© AW
Komponenty |
Segway – trochę matmy, trochę fizy
Wiemy już jak się na Segway'u poruszać i co w nim siedzi. Jak to się jednak wszystko dzieje, jakie prawa tu działają? Zapraszamy do lektury ostatniej części z cyklu, opisującego ten niezwykły pojazd.
Ogólną zasadę działania pojazdu ilustruje poniższy rysunek (Rys1). Właściwą sytuacją jest utrzymanie drążka (a więc i pasażera) w pozycji pionowej (prostopadłej do powierzchni ziemii). Jednakże obiekty w naszym świecie nie są idealne i działają na nie różne siły, może to być drgający pasażer, podmuch wiatru, złe wyważenie, bezwładność, niedokładność pracy silników, i wiele innych czynników.
 © Adam W.
Pod ich wpływem, drążek (a więc i pasażer) przechylają się w jedną, bądź drugą stronę. Następuje więc powolny przewrót (zakładamy) w przód. Prędkość tego opadania rośnie, a jej wartość chwilą określa Θp. Aby zniwelować ten przechył, należy uruchomić silniki w taki sposób, by wywołały one ruch posuwisty w stronę opadania drążka (przy naszych założeniach – w przód). Prędkość obrotowa kół uzależniona jest od prędkości opadania, a więc obecnego kąta przechyłu. Ruch silników wywołuje ruch posuwisty pojazdu do przodu – υ.
Jednakże fizyka, jest nieco bardziej skomplikowana. W sieci można znaleźć szereg publikacji traktujących o problemie wahadła odwróconego, w tym też przypadku, kiedy to podstawa jezdna jest w formie silników z kołami (segway).
© Adam W.
Pod ich wpływem, drążek (a więc i pasażer) przechylają się w jedną, bądź drugą stronę. Następuje więc powolny przewrót (zakładamy) w przód. Prędkość tego opadania rośnie, a jej wartość chwilą określa Θp. Aby zniwelować ten przechył, należy uruchomić silniki w taki sposób, by wywołały one ruch posuwisty w stronę opadania drążka (przy naszych założeniach – w przód). Prędkość obrotowa kół uzależniona jest od prędkości opadania, a więc obecnego kąta przechyłu. Ruch silników wywołuje ruch posuwisty pojazdu do przodu – υ.
Jednakże fizyka, jest nieco bardziej skomplikowana. W sieci można znaleźć szereg publikacji traktujących o problemie wahadła odwróconego, w tym też przypadku, kiedy to podstawa jezdna jest w formie silników z kołami (segway).
 © Adam W.
System wahadła odwróconego, zaaplikowanego do pojazdu jednoosiowego, przeanalizujmy z uwzględnieniem liniowego modelu silników. Najpierw uzyskamy modele dla poszczególnych kół, a następnie dla całej konstrukcji pojazdu.
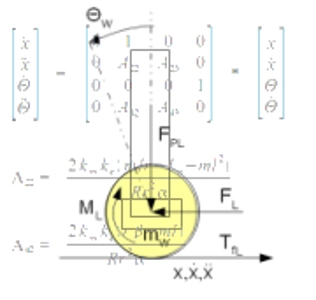
Siły F_R i F_L są siłami reakcji obciążenia, a F_PR i F_PL są siłami reakcji pomiędzy kołami a wózkiem. T_fR i T_fL to siły tarcia, M_R i M_L to moment napędzający każde z kół, z kolei m_w to masa koła.
Analizując lewe koło, suma sił w osi równoległej dla koła prawego w stosunku do podłoża, wynosi zgodnie z prawem Newton'a wzór (1).
© Adam W.
System wahadła odwróconego, zaaplikowanego do pojazdu jednoosiowego, przeanalizujmy z uwzględnieniem liniowego modelu silników. Najpierw uzyskamy modele dla poszczególnych kół, a następnie dla całej konstrukcji pojazdu.
Siły F_R i F_L są siłami reakcji obciążenia, a F_PR i F_PL są siłami reakcji pomiędzy kołami a wózkiem. T_fR i T_fL to siły tarcia, M_R i M_L to moment napędzający każde z kół, z kolei m_w to masa koła.
Analizując lewe koło, suma sił w osi równoległej dla koła prawego w stosunku do podłoża, wynosi zgodnie z prawem Newton'a wzór (1).
 © Adam W.
Suma momentów wokół środka koła opisano następującym równaniem (2). Wyjściowy moment napędowy dla każdego z kół przedstawiony został za pomocą wzoru (3), gdzie indukcyjność i tarcie w silnikach pominięto, R jest nominalną rezystancją termiczną [Ω]. Prędkość obrotowa na silnikach jest transformowana na ruch liniowy zgodnie z równaniem (4) i (5). Przedstawione równania dla koła prawego można przenieść dla koła lewego, gdyż sytuacje i siły na te koła działające są takie same, w przypadku analizowanego ruchu w ustalonym kierunku. W wyniku transformacji powyższych równań otrzymujemy równianie (6).
© Adam W.
Suma momentów wokół środka koła opisano następującym równaniem (2). Wyjściowy moment napędowy dla każdego z kół przedstawiony został za pomocą wzoru (3), gdzie indukcyjność i tarcie w silnikach pominięto, R jest nominalną rezystancją termiczną [Ω]. Prędkość obrotowa na silnikach jest transformowana na ruch liniowy zgodnie z równaniem (4) i (5). Przedstawione równania dla koła prawego można przenieść dla koła lewego, gdyż sytuacje i siły na te koła działające są takie same, w przypadku analizowanego ruchu w ustalonym kierunku. W wyniku transformacji powyższych równań otrzymujemy równianie (6).
 © Adam W.
W tym przypadku rozpatrując konstrukcję nośną, wraz z obciążeniem posłużono się prawem Newtona dla opisu sił działających w osi poziomej, w kartezjańskim układzie współrzędnych, przyjętych w tych rozważaniach (7). Z kolei suma sił działająca prostopadle do konstrukcji określona została jako (8).
© Adam W.
W tym przypadku rozpatrując konstrukcję nośną, wraz z obciążeniem posłużono się prawem Newtona dla opisu sił działających w osi poziomej, w kartezjańskim układzie współrzędnych, przyjętych w tych rozważaniach (7). Z kolei suma sił działająca prostopadle do konstrukcji określona została jako (8).
 © Adam W.
Suma momentów wokół środka masy konstrukcji rozpatrywanej jako wahadło (9). Mnożąc równanie (8) przez „-l” i odejmując stronami z równaniem (9) otrzymano (10). Natomiast odejmując (7) od (6) stronami otrzymamy (11). W wyniku naszych działań otrzymaliśmy równania (10) i (11), które są nieliniowe.
Możemy jednakże to uprościć, stosując model liniowy i zlinearyzować te równania. Zgodnie z zasadą, że dla małych katów, sinus tego kąta równa się danemu kątowi przyjęto następujące uproszczenia (12-15). W konsekwencji tych założeń otrzymujemy macierz (16), której współczynniki przedstawiają się tak, jak podano w równaniach (17) i (18).
Sporo tych przedziwnych równań, jednakże jest to stosunkowo uproszczony model matematyczny Segwaya. Jak już wspomniano, posłużyliśmy się modelem liniowym, a w przyrodzie, niestety nic nie jest liniowe. W rzeczywistości, zachowanie tego pojazdu jest jeszcze bardziej skomplikowane, stąd w oryginalnym pojeździe mnogość różnego rodzaju mikrokontrolerów.
Jednakże, dla uproszczenia można przyjąć, że napięcie, jakie należy podać na silniki, prezentuje się mniej więcej tak:
© Adam W.
Suma momentów wokół środka masy konstrukcji rozpatrywanej jako wahadło (9). Mnożąc równanie (8) przez „-l” i odejmując stronami z równaniem (9) otrzymano (10). Natomiast odejmując (7) od (6) stronami otrzymamy (11). W wyniku naszych działań otrzymaliśmy równania (10) i (11), które są nieliniowe.
Możemy jednakże to uprościć, stosując model liniowy i zlinearyzować te równania. Zgodnie z zasadą, że dla małych katów, sinus tego kąta równa się danemu kątowi przyjęto następujące uproszczenia (12-15). W konsekwencji tych założeń otrzymujemy macierz (16), której współczynniki przedstawiają się tak, jak podano w równaniach (17) i (18).
Sporo tych przedziwnych równań, jednakże jest to stosunkowo uproszczony model matematyczny Segwaya. Jak już wspomniano, posłużyliśmy się modelem liniowym, a w przyrodzie, niestety nic nie jest liniowe. W rzeczywistości, zachowanie tego pojazdu jest jeszcze bardziej skomplikowane, stąd w oryginalnym pojeździe mnogość różnego rodzaju mikrokontrolerów.
Jednakże, dla uproszczenia można przyjąć, że napięcie, jakie należy podać na silniki, prezentuje się mniej więcej tak:
 © Adam W.
k1 i k2 to pewne, dobrane indywidualnie, często doświadczalnie, współczynniki. 'W' to nasze wychylenie odczytane z akcelerometru, a 'P' to prędkość opadania drążka mierzona żyroskopem. Z tego właśnie równania korzystają amatorzy, budujące swoje konstrukcje na wzór Segwaya.
Ten, jak i pozostałe artykuły z tej serii objęte są prawami autorskimi. Powielanie ich bez zgodny autora jest nielegalne. Mają one jedynie charakter edukacjny.
© Adam W.
k1 i k2 to pewne, dobrane indywidualnie, często doświadczalnie, współczynniki. 'W' to nasze wychylenie odczytane z akcelerometru, a 'P' to prędkość opadania drążka mierzona żyroskopem. Z tego właśnie równania korzystają amatorzy, budujące swoje konstrukcje na wzór Segwaya.
Ten, jak i pozostałe artykuły z tej serii objęte są prawami autorskimi. Powielanie ich bez zgodny autora jest nielegalne. Mają one jedynie charakter edukacjny.
 © Adam W.
Pod ich wpływem, drążek (a więc i pasażer) przechylają się w jedną, bądź drugą stronę. Następuje więc powolny przewrót (zakładamy) w przód. Prędkość tego opadania rośnie, a jej wartość chwilą określa Θp. Aby zniwelować ten przechył, należy uruchomić silniki w taki sposób, by wywołały one ruch posuwisty w stronę opadania drążka (przy naszych założeniach – w przód). Prędkość obrotowa kół uzależniona jest od prędkości opadania, a więc obecnego kąta przechyłu. Ruch silników wywołuje ruch posuwisty pojazdu do przodu – υ.
Jednakże fizyka, jest nieco bardziej skomplikowana. W sieci można znaleźć szereg publikacji traktujących o problemie wahadła odwróconego, w tym też przypadku, kiedy to podstawa jezdna jest w formie silników z kołami (segway).
© Adam W.
Pod ich wpływem, drążek (a więc i pasażer) przechylają się w jedną, bądź drugą stronę. Następuje więc powolny przewrót (zakładamy) w przód. Prędkość tego opadania rośnie, a jej wartość chwilą określa Θp. Aby zniwelować ten przechył, należy uruchomić silniki w taki sposób, by wywołały one ruch posuwisty w stronę opadania drążka (przy naszych założeniach – w przód). Prędkość obrotowa kół uzależniona jest od prędkości opadania, a więc obecnego kąta przechyłu. Ruch silników wywołuje ruch posuwisty pojazdu do przodu – υ.
Jednakże fizyka, jest nieco bardziej skomplikowana. W sieci można znaleźć szereg publikacji traktujących o problemie wahadła odwróconego, w tym też przypadku, kiedy to podstawa jezdna jest w formie silników z kołami (segway).
 © Adam W.
System wahadła odwróconego, zaaplikowanego do pojazdu jednoosiowego, przeanalizujmy z uwzględnieniem liniowego modelu silników. Najpierw uzyskamy modele dla poszczególnych kół, a następnie dla całej konstrukcji pojazdu.
Siły F_R i F_L są siłami reakcji obciążenia, a F_PR i F_PL są siłami reakcji pomiędzy kołami a wózkiem. T_fR i T_fL to siły tarcia, M_R i M_L to moment napędzający każde z kół, z kolei m_w to masa koła.
Analizując lewe koło, suma sił w osi równoległej dla koła prawego w stosunku do podłoża, wynosi zgodnie z prawem Newton'a wzór (1).
© Adam W.
System wahadła odwróconego, zaaplikowanego do pojazdu jednoosiowego, przeanalizujmy z uwzględnieniem liniowego modelu silników. Najpierw uzyskamy modele dla poszczególnych kół, a następnie dla całej konstrukcji pojazdu.
Siły F_R i F_L są siłami reakcji obciążenia, a F_PR i F_PL są siłami reakcji pomiędzy kołami a wózkiem. T_fR i T_fL to siły tarcia, M_R i M_L to moment napędzający każde z kół, z kolei m_w to masa koła.
Analizując lewe koło, suma sił w osi równoległej dla koła prawego w stosunku do podłoża, wynosi zgodnie z prawem Newton'a wzór (1).
 © Adam W.
Suma momentów wokół środka koła opisano następującym równaniem (2). Wyjściowy moment napędowy dla każdego z kół przedstawiony został za pomocą wzoru (3), gdzie indukcyjność i tarcie w silnikach pominięto, R jest nominalną rezystancją termiczną [Ω]. Prędkość obrotowa na silnikach jest transformowana na ruch liniowy zgodnie z równaniem (4) i (5). Przedstawione równania dla koła prawego można przenieść dla koła lewego, gdyż sytuacje i siły na te koła działające są takie same, w przypadku analizowanego ruchu w ustalonym kierunku. W wyniku transformacji powyższych równań otrzymujemy równianie (6).
© Adam W.
Suma momentów wokół środka koła opisano następującym równaniem (2). Wyjściowy moment napędowy dla każdego z kół przedstawiony został za pomocą wzoru (3), gdzie indukcyjność i tarcie w silnikach pominięto, R jest nominalną rezystancją termiczną [Ω]. Prędkość obrotowa na silnikach jest transformowana na ruch liniowy zgodnie z równaniem (4) i (5). Przedstawione równania dla koła prawego można przenieść dla koła lewego, gdyż sytuacje i siły na te koła działające są takie same, w przypadku analizowanego ruchu w ustalonym kierunku. W wyniku transformacji powyższych równań otrzymujemy równianie (6).
 © Adam W.
W tym przypadku rozpatrując konstrukcję nośną, wraz z obciążeniem posłużono się prawem Newtona dla opisu sił działających w osi poziomej, w kartezjańskim układzie współrzędnych, przyjętych w tych rozważaniach (7). Z kolei suma sił działająca prostopadle do konstrukcji określona została jako (8).
© Adam W.
W tym przypadku rozpatrując konstrukcję nośną, wraz z obciążeniem posłużono się prawem Newtona dla opisu sił działających w osi poziomej, w kartezjańskim układzie współrzędnych, przyjętych w tych rozważaniach (7). Z kolei suma sił działająca prostopadle do konstrukcji określona została jako (8).
 © Adam W.
Suma momentów wokół środka masy konstrukcji rozpatrywanej jako wahadło (9). Mnożąc równanie (8) przez „-l” i odejmując stronami z równaniem (9) otrzymano (10). Natomiast odejmując (7) od (6) stronami otrzymamy (11). W wyniku naszych działań otrzymaliśmy równania (10) i (11), które są nieliniowe.
Możemy jednakże to uprościć, stosując model liniowy i zlinearyzować te równania. Zgodnie z zasadą, że dla małych katów, sinus tego kąta równa się danemu kątowi przyjęto następujące uproszczenia (12-15). W konsekwencji tych założeń otrzymujemy macierz (16), której współczynniki przedstawiają się tak, jak podano w równaniach (17) i (18).
Sporo tych przedziwnych równań, jednakże jest to stosunkowo uproszczony model matematyczny Segwaya. Jak już wspomniano, posłużyliśmy się modelem liniowym, a w przyrodzie, niestety nic nie jest liniowe. W rzeczywistości, zachowanie tego pojazdu jest jeszcze bardziej skomplikowane, stąd w oryginalnym pojeździe mnogość różnego rodzaju mikrokontrolerów.
Jednakże, dla uproszczenia można przyjąć, że napięcie, jakie należy podać na silniki, prezentuje się mniej więcej tak:
© Adam W.
Suma momentów wokół środka masy konstrukcji rozpatrywanej jako wahadło (9). Mnożąc równanie (8) przez „-l” i odejmując stronami z równaniem (9) otrzymano (10). Natomiast odejmując (7) od (6) stronami otrzymamy (11). W wyniku naszych działań otrzymaliśmy równania (10) i (11), które są nieliniowe.
Możemy jednakże to uprościć, stosując model liniowy i zlinearyzować te równania. Zgodnie z zasadą, że dla małych katów, sinus tego kąta równa się danemu kątowi przyjęto następujące uproszczenia (12-15). W konsekwencji tych założeń otrzymujemy macierz (16), której współczynniki przedstawiają się tak, jak podano w równaniach (17) i (18).
Sporo tych przedziwnych równań, jednakże jest to stosunkowo uproszczony model matematyczny Segwaya. Jak już wspomniano, posłużyliśmy się modelem liniowym, a w przyrodzie, niestety nic nie jest liniowe. W rzeczywistości, zachowanie tego pojazdu jest jeszcze bardziej skomplikowane, stąd w oryginalnym pojeździe mnogość różnego rodzaju mikrokontrolerów.
Jednakże, dla uproszczenia można przyjąć, że napięcie, jakie należy podać na silniki, prezentuje się mniej więcej tak:
 © Adam W.
k1 i k2 to pewne, dobrane indywidualnie, często doświadczalnie, współczynniki. 'W' to nasze wychylenie odczytane z akcelerometru, a 'P' to prędkość opadania drążka mierzona żyroskopem. Z tego właśnie równania korzystają amatorzy, budujące swoje konstrukcje na wzór Segwaya.
Ten, jak i pozostałe artykuły z tej serii objęte są prawami autorskimi. Powielanie ich bez zgodny autora jest nielegalne. Mają one jedynie charakter edukacjny.
© Adam W.
k1 i k2 to pewne, dobrane indywidualnie, często doświadczalnie, współczynniki. 'W' to nasze wychylenie odczytane z akcelerometru, a 'P' to prędkość opadania drążka mierzona żyroskopem. Z tego właśnie równania korzystają amatorzy, budujące swoje konstrukcje na wzór Segwaya.
Ten, jak i pozostałe artykuły z tej serii objęte są prawami autorskimi. Powielanie ich bez zgodny autora jest nielegalne. Mają one jedynie charakter edukacjny.